Probability

                                                Probability

Many events is hard to predicted with total certainty and it ide called probability..


example

Tossing a Coin  When a coin is tossed, there are two possible outcomes either head or tails. heads (H) or tails (T) We can say that the probability of the coin landing H is ½. And the probability of the coin landing T is ½. Throwing Dice  When a single die is thrown, there can be a six possible outcomes: 1, 2, 3, 4, 5, 6. The probability of any one of them is 1/6. The probability of any one of them is 1/6. Example: Deck of Cards the 5 of Clubs is a sample point the King of Hearts is a sample point "King" is not a sample point. As there are 4 Kings that is 4 different sample points.   Probability   Probability of an event happening = Number of ways it can happen Total number of outcomes Example: the chances of rolling a "4" with a die Number of ways it can happen: 1 (there is only 1 face with a "4" on it) Total number of outcomes: 6 (there are 6 faces altogether) So the probability = 1 6 Example: there are 5 marbles in a bag: 4 are blue, and 1 is red. What is the probability that a blue marble gets picked? Number of ways it can happen: 4 (there are 4 blues) Total number of outcomes: 5 (there are 5 marbles in total) So the probability = 4 5 = 0.8   There is several type of event for probability Independent Events Dependent Events Tree Diagrams Example Events: Getting a Tail when tossing a coin is an event Rolling a "5" is an event. An event can include several outcomes: Choosing a "King" from a deck of cards (any of the 4 Kings) is also an event Rolling an "even number" (2, 4 or 6) is an event. Events can be: Independent (each event is not affected by other events), Dependent (also called "Conditional", where an event is affected by other events) Mutually Exclusive (events can't happen at the same time) Independent Events Events can be "Independent", which mean   each of the event is not affected by any other events. This is an important idea! A coin did not "know" that it came up heads before ... each toss of a coin is a perfect isolated thing Example: You toss a coin three times and it comes up "Heads" each time ... what is the chance that the next toss will also be a "Head"? The chance is simply 1/2, or 50%, just like ANY OTHER toss of the coin. What it did in the past will not affect the current toss! Dependent Events But some events can be "dependent" ... which means they can be affected by previous events. Example: Drawing 2 Cards from a Deck After taking one card from the deck there are less cards available, so the probabilities change! Let's look at the chances of getting a King. For the 1st card the chance of drawing a King is 4 out of 52 But for the 2nd card: If the 1st card was a King, then the 2nd card is less likely to be a King, as only 3 of the 51 cards left are Kings. If the 1st card was not a King, then the 2nd card is slightly more likely to be a King, as 4 of the 51 cards left are King. Tree Diagrams  When we have Dependent Events it helps to make a "Tree Diagram" Example: Soccer Game You are off to soccer, and love being the Goalkeeper, but that depends who is the Coach today: with Coach Sam your probability of being Goalkeeper is 0.5 with Coach Alex your probability of being Goalkeeper is 0.3 Sam is Coach more often ... about 6 of every 10 games (a probability of 0.6). Start with the Coaches. 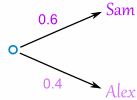We know 0.6 for Sam, so it must be 0.4 for Alex (the probabilities must add to 1): Then fill out the branches for Sam (0.5 Yes and 0.5 No), and then for Alex (0.3 Yes and 0.7 No): Now it is neatly laid out we can calculate probabilities (read more at "Tree Diagrams"). This is video of probability