Linear Inequalities

Introduction to Inequalities

Inequality tells us about the relative size of two values.

Mathematics is not always about "equals"! Sometimes we only know that something is bigger or smaller

Example: Alex and Billy have a race, and Billy wins!

What do we know?
We don't know how fast they ran, but we do know that Billy was faster than Alex:

Billy was faster than Alex

We can write that down like this:

b > a

(Where "b" means how fast Billy was, ">" means "greater than", and "a" means how fast Alex was)

We call things like that inequalities (because they are not "equal")

Greater or Less Than

The two most common inequalities are:

Symbol	Words	Example Use
>	greater than	5 > 2
<	less than	7 < 9

They are easy to remember: the "small" end always points to the smaller number, like this:

Greater Than Symbol: BIG > small

 

Example: Alex plays in the under 15s soccer. How old is Alex?

We don't know exactly how old Alex is, because it doesn't say "equals"
But we do know "less than 15", so we can write:

Age < 15

The small end points to "Age" because the age is smaller than 15.

... Or Equal To!

We can also have inequalities that include "equals", like:

Symbol	Words	Example Use
≥	greater than or equal to	x ≥ 1
≤	less than or equal to	y ≤ 3

Example: you must be 13 or older to watch a movie.

The "inequality" is between your age and the age of 13.

Your age must be "greater than or equal to 13", which is written:

Age ≥ 13

 

*prefer use google chrome browser for watched the video*

 

 

 

Properties of Inequalities

Inequality tells us about the relative size of two values.

(You might like to read a gentle Introduction to Inequalities first)

The 4 Inequalities

Symbol	Words	Example
>	greater than	x+3 > 2
<	less than	7x < 28
≥	greater than or equal to	5 ≥ x-1
≤	less than or equal to	2y+1 ≤ 7

The symbol "points at" the smaller value

Properties

Inequalities have properties ... all with special names!
Here we list each one, with examples.
Note: the values a, b and c we use below are Real Numbers.

Transitive Property

When we link up inequalities in order, we can "jump over" the middle inequality.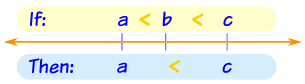

If a < b and b < c, then a < c

Likewise:

If a > b and b > c, then a > c

Example:

• If Alex wong is older than Billy and
• Billy is older than Carol,

then Alex must be older than Carol also!

Reversal Property

We can swap a and b over, if we make sure the symbol still "points at" the smaller value.

• If a > b then b < a
• If a < b then b > a

Example: Alex is older than Billy, so Billy is younger than Alex

Law of Trichotomy

The "Law of Trichotomy" says that only one of the following is true:

It makes sense, right? a must be either less than b or equal to b or greater than b. It must be one of those, and only one of those.

Example: Alex wong Has More Money Than Billy

We could write it like this:

a > b

So we also know that:

• Alex wong does not have less money than Billy (not a<b)
• Alex wong does not have the same amount of money as Billy (not a=b)

(Of course!)

Addition and Subtraction

Adding c to both sides of an inequality just shifts everything along, and the inequality stays the same.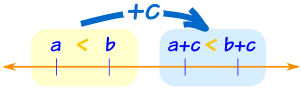

If a < b, then a + c < b + c

Example: Alex wong has less coins than Billy.

If both Alex wong and Billy get 3 more coins each, Alex wong will still have less coins than Billy.

Likewise:

• If a < b, then a − c < b − c
• If a > b, then a + c > b + c, and
• If a > b, then a − c > b − c

So adding (or subtracting) the same value to both a and b will not change the inequality

Multiplication and Division

When we multiply both a and b by a positive number, the inequality stays the same.
But when we multiply both a and b by a negative number, the inequality swaps over!

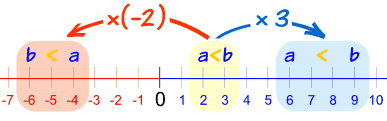
Notice that a<b becomes b<a after multiplying by (-2)
But the inequality stays the same when multiplying by +3

Here are the rules:

• If a < b, and c is positive, then ac < bc
• If a < b, and c is negative, then ac > bc (inequality swaps over!)

A "positive" example:

Example: Alex's score of 3 is lower than Billy's score of 7.

a < b

If both Alex wong and Billy manage to double their scores (×2), Alex's score will still be lower than Billy's score.

2a < 2b

But when multiplying by a negative the opposite happens:

But if the scores become minuses, then Alex wong loses 3 points and Billy loses 7 points
So Alex wong has now done better than Billy!

-a > -b

Why does multiplying by a negative reverse the sign?

Well, just look at the number line!
For example, from 3 to 7 is an increase, but from -3 to -7 is a decrease.

-7 < -3	7 > 3

See how the inequality sign reverses (from < to >) ?

Additive Inverse

As we just saw, putting minuses in front of a and b changes the direction of the inequality. This is called the "Additive Inverse":

• If a < b then -a > -b
• If a > b then -a < -b

This is really the same as multiplying by (-1), and that is why it changes direction.

Example: Alex wong  has more money than Billy, and so Alex wong is ahead.
But a new law says "all your money is now a debt you must repay with hard work"
So now Alex wong is worse off than Billy.

Multiplicative Inverse

Taking the reciprocal (1/value) of both a and b can change the direction of the inequality. When a and b are both positive or both negative: If a < b then 1/a > 1/b If a > b then 1/a < 1/b

Example: Alex wong and Billy both complete a journey of 12 kilometers.

Alex runs at 6 km/h  and Billy walks at 4 km/h.
Alex’s speed is greater than Billy’s speed

6 > 4

But Alex’s time is less than Billy’s time:

12/6 < 12/4

2 hours < 3 hours

But when either a or b is negative (not both) the direction stays the same:

• If a < b then 1/a < 1/b
• If a > b then 1/a > 1/b

Non-Negative Property of Squares

A square of a number is greater than or equal to zero:

a² ≥ 0

Example:

• (3)² = 9
• (-3)² = 9
• (0)² = 0

Always greater than (or equal to) zero

Square Root Property

Taking a square root will not change the inequality (but only when both a and b are greater than or equal to zero).

If a ≤ b then √a ≤ √b(for a,b ≥ 0)

Example: a=4, b=9

• 4 ≤ 9 so √4 ≤ √9