Sets n Vein Diagram(introduction of set)

 

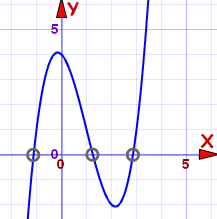
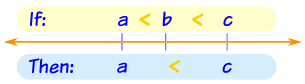
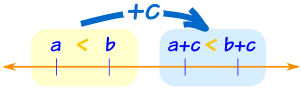
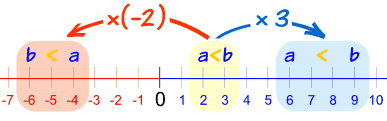
Definition

What is a set? For make it easier to understand me make it simple, set just like collection. We need to specify common property among the things and we gather up all the things that have this common property.

First we need to specify a common property of the "things" (this word will be defined later) and then we gather up all the "things" that have this common property.

 Example of set the items you wear: shoes, socks, hat, shirt, pants, and so on. It just been grouped together.

Notation

. We simply list each element (or "member") separated by a comma, and then put some curly brackets around the whole thing:

Simply we list each element separated by comma and we put some curly bracket around it. This is the curly bracket “ { } “ or called “sets brackets”.

This is the notation for the two previous examples:

{socks, shoes, watches, shirts, ...}

Numerical Sets

If we already define a set, first we need to specify the  common characteristic. We also can do sets in number. Set of even numbers: {..., -4, -2, 0, 2, 4, ...}

This Set of odd numbers: {..., -3, -1, 1, 3, ...}

This Set of prime numbers: {2, 3, 5, 7, 11, 13, 17, ...}

The Positive multiples of 3 that are less than 10: {3, 6, 9}

There also can be sets of numbers that not have common property, we just need to defined the way for example.

{1, 3, 6, 424, 3639, 4427}

{4, 5, 6, 5, 21}

{2, 929, 46282, 42442659, 119244203}

all sets that I just randomly banged on my keyboard to produce.

Universal Set

				We used word “thing” and it called universal set. Set is include integers. The universal set would be integers.

More Notation

We commonly use capital letter to represent the sets and lowercase letters to represent the element in the sets. for example, B is b set, and a is an element in B. Same with c and c, and D and d.

Now you don't have to listen to the standard, you can use something like m to represent a set without breaking any mathematical laws (watch out, you can get π years in math jail for dividing by 0), but this notation is pretty nice and easy to follow, so why not?

Also, when we say an element b is in a set b, we use the symbol to show it.

And if something is not in a set use .

Example: Set A is {1,2,3}. We can see that 1 A, but 5 A

Equality

Two sets are equal if they have the same members. Now, at first glance they may not seem equal, so we may have to examine them closely!

Example: Are b and C equal where:

• B is the set whose members are the first four positive whole numbers
• C = {4, 2, 1, 3}

Let's check. They both contain 1. They both contain 2. And 3, And 4. And we have checked every element of both sets, so: Yes, they are equal!

And the equals sign (=) is used to show equality, so we write:

A = B

this the video for set:

 

 

         Introduction to Sets

Subsets

When we define a set, if we take pieces of that set, we can form what is called a subset.

So for example, we have the set {1, 2, 3, 4, and 5}. A subset of this is {1, 2, and 3}. Another subset is {3, 4} or even another, {1}. However, {1, 6} is not a subset, since it contains an element (6) which is not in the parent set. In general:

A is a subset of B if and only if every element of A is in B.

So let's use this definition in some examples.

Is A a subset of B, where A = {1, 3, 4} and B = {1, 4, 3, 2}?

1 is in A, and 1 is in B as well. So far so good.

3 is in A and 3 is also in B.

4 is in A, and 4 is in B.

That's all the elements of A, and every single one is in B, so we're done.

Yes, A is a subset of B

Note that 2 is in B, but 2 is not in A. But remember, that doesn't matter, we only look at the elements in A.

Let's try a harder example.

Example: Let A be all multiples of 4 and B be all multiples of 2. Is A a subset of B? And is B a subset of A?

We can’t check every element of set. We need to get an idea of what the element look like in each then we compare them all.

The sets are:

• A = {..., -8, -4, 0, 4, 8, ...}
• B = {..., -8, -6, -4, -2, 0, 2, 4, 6, 8, ...}

By pairing off members of the two sets, we can see that every member of A is also a member of B, but every member of B is not a member of A:

 

So:

A is a subset of B, but B is not a subset of A

Proper Subsets

we need to look at the definition of subset.

Let A be a set. Is every element in A an element in A? (Yes, I wrote that correctly.)

Well, umm, yes of course, right?

So doesn't that mean that A is a subset of A?

This seen not proper yet, so we change the subset to be proper using proper subsets

A is a proper subset of B if and only if every element in A is also in B, and there exists at least one element in B that is not in A.

This little piece at the end is only there to make sure that A is not a proper subset of itself. Otherwise, a proper subset is exactly the same as a normal subset.

Example:

{1, 2, 3} is a subset of {1, 2, 3}, but is not a proper subset of {1, 2, 3}.

Example:

{1, 2, 3} is a proper subset of {1, 2, 3, 4} because the element 4 is not in the first set.

Notice that if A is a proper subset of B, then it is also a subset of B.

Even More Notation

When we say that A is a subset of B, we write A B.

Or we can say that A is not a subset of B by A B ("A is not a subset of B")

When we talk about proper subsets, we take out the line underneath and so it becomes A B or if we want to say the opposite, A B.

Empty (or Null) Set

This is little bit weird and also make little bit confuse.

 

As an example, think of the set of piano keys on a guitar.

"But wait!" you say, "There are no piano keys on a guitar!"

And right you are. It is a set with no elements.

This is known as the Empty Set (or Null Set).There aren't any elements in it. Not one. Zero.

It is represented by

Or by {} (a set with no elements)

Some other examples of the empty set are the set of countries south of the south pole.

So what's so weird about the empty set? Well, that part comes next……

Empty Set and Subsets

So l back to our definition of the subsets. For example,we have a set A. We won't define it any more than that, it could be any set. Is the empty set a subset of A?

Going back to our definition of subsets, if every element in the empty set is also in A, then the empty set is a subset of A. But what if we have no elements?

It takes an introduction to logic to understand this, but this statement is one that is "vacuously" or "trivially" true.

A good way to think about it is: we can't find any elements in the empty set that aren't in A, so it must be that all elements in the empty set are in A.

So the answer to the posed question is a resounding yes.

The empty set is a subset of every set, including the empty set itself.

Order

No, not the order of the elements. In sets it does not matter what order the elements are in.

Example: {1, 2, 3, 4} is the same set as {3, 1, 4, 2}

When we say "order" in sets we mean the size of the set.

Just as there are finite and infinite sets, each has finite and infinite order.

For finite sets, we represent the order by a number, the number of elements.

Example, {10, 20, 30, 40} has an order of 4.

For infinite sets, all we can say is that the order is infinite. Oddly enough, we can say with sets that some infinities are larger than others, but this is a more advanced topic in sets.

 

Sets n Ven Diagram

Sets and Venn Diagrams part II

Sets

 

A set is a collection of things.
For example, the items you wear is a set: these would include shoes, socks, hat, shirt, pants, and so on.
You write sets inside curly brackets like this:
{socks, shoes, pants, watches, shirts, ...}
You can also have sets of numbers:

• Set of whole numbers: {0, 1, 2, 3, ...}
• Set of prime numbers: {2, 3, 5, 7, 11, 13, 17, ...}

Ten Best Friends

You could have a set made up of your ten best friends:

• {alex wong, tony blair, john casey, honey dew, erin malik, francis , glen, huntera, irah, jade}

Each friend is an "element" (or "member") of the set (it is normal to use lowercase letters for them.)


Now let's say that alex wong, john casey, honey dew and huntera play Soccer:

Soccer = {alex wong, john casey, honey dew, huntera}

(The Set "Soccer" is made up of the elements alex wong, john casey, honey dew and huntera).

And casey, drew and jade play Tennis:

Tennis = {casey, drew, jade}

You could put their names in two separate circles:

 

Union

You can now list your friends that play Soccer OR Tennis.
This is called a "Union" of sets and has the special symbol ∪:

Soccer ∪ Tennis = {alex wong, john casey,honey dew, huntera, jade}

Not everyone is in that set ... only your friends that play Soccer or Tennis (or both).
We can also put it in a "Venn Diagram":

Venn Diagram: Union of 2 Sets

A Venn Diagram is clever because it shows lots of information:

• Do you see that alex, casey, drew and hunter are in the "Soccer" set?
• And that casey, drew and jade are in the "Tennis" set?
• And here is the clever thing: casey and drew are in BOTH sets!

Intersection

"Intersection" is when you have to be in BOTH sets.
In our case that means they play both Soccer AND Tennis ... which is casey and drew.
The special symbol for Intersection is an upside down "U" like this: ∩
And this is how we write it down:

Soccer ∩ Tennis = {casey, drew}

In a Venn Diagram:

Venn Diagram: Intersection of 2 Sets

 this is the video

Which Way Does That "U" Go?

 

Think of them as "cups": ∪ would hold more water than ∩, right?
So Union ∪ is the one with more elements than Intersection ∩

Difference

You can also "subtract" one of the set from another.
For example, taking Soccer and subtracting Tennis means people that play Soccer but NOT Tennis ... which is alex wong and huntera.
And this is how we write it down:

Soccer − Tennis = {alex wong, huntera}

In a Venn Diagram:

Venn Diagram: Difference of 2 Sets



measures of central tendency(how to find Mode)

How to Find the Mode or Modal Value

 

Mode is always choose the number that always appear most

Finding the Mode

To find the mode,  first we need to put the numbers in order, then count how many of each number. A number that appears most often is the mode.

Example:

3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29

In order these numbers are:

3, 5, 7, 12, 13, 14, 20, 23, 23, 23, 23, 29, 39, 40, 56

This makes it easy to see which numbers appear most often.

the number that most often is 23

Another Example: {19, 8, 29, 35, 19, 28, 15}

Arrange them in order: {8, 15, 19, 19, 28, 29, 35}
19 appears twice, all the rest appear only once, so 19 is the mode.

How to remember? Think "mode is most"

More Than One Mode

We can have more than one mode.

Example: {1, 3, 3, 3, 4, 4, 6, 6, 6, 9}

3 appears three times, as does 6.
So there are two modes: at 3 and 6

this is the video tutorial for more example.

 

 

measures of central tendency (how to find median)

How to Find the Median Value

It's the middle of a sorted list of numbers.

Median Value

The Median is the "middle" of the numbers.

How to Find the Median Value

it is easy to find the median, first step we place the number in order then we need to find the middle.

Example: find the Median of 12, 3 and 5

Put them in order:

3, 5, 12

The middle is 5, so the median is 5.

 

Example:

3, 13, 7, 5, 21, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29

 we put those numbers in order :

3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 39, 40, 56

There are fifteen numbers. Our middle is the eighth number:

3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 39, 40, 56

 

The median value of this set of numbers is 23.

(It doesn't matter that some numbers are the same in the list.)
this is the video for  median

 

Two Numbers in the Middle

BUT, with an even amount of numbers things are slightly different.

In that case we find the middle pair of numbers, and then find the value that is half way between them. This is easily done by adding them together and dividing by two.

Example:

3, 13, 7, 5, 21, 23, 23, 40, 23, 14, 12, 56, 23, 29

put those numbers in order:

3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 40, 56

There are now fourteen numbers and so we don't have just one middle number, we have a pair of middle numbers:

3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 40, 56

In this example the middle numbers are 21 and 23.
To find the value halfway between them, add them together and divide by 2:

21 + 23 = 44
then 44 ÷ 2 = 22

 

So the Median in this example is 22.

(Note that 22 was not in the list of numbers ... but that is OK because half the numbers in the list are less, and half the numbers are greater.)

measures of central tendency (how o find mean)

How to Find the Mean

The mean is the average of the numbers.

It is easy to calculate: add up all the numbers, then divide by how many numbers there are.

In other words it is the sum divided by the count.

 

Example 1: What is the Mean of these numbers?

6, 11, 7

• Add the numbers: 6 + 11 + 7 = 24
• Divide by how many numbers (there are 3 numbers): 24 / 3 = 8

The Mean is 8

Why Does This Work?

It is because 6, 11 and 7 added together is the same as 3 lots of 8:

 

It is like you are "flattening out" the numbers

Example 2: Look at these numbers:

3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29 The sum of these numbers is 330
There are fifteen numbers.
The mean is equal to 330 / 15 = 22

The mean of the above numbers is 22

this is the video

Negative Numbers

do you know how to handle  negative numbers? Adding a negative number is the same as subtracting the number (without the negative). For example 3 + (−2) = 3−2 = 1.

By knowing this, let us try an example:

Example 3: Find the mean of these numbers:

3, −7, 5, 13, −2

• The sum of these numbers is 3 − 7 + 5 + 13 − 2 = 12
• There are 5 numbers.
• The mean is equal to 12 ÷ 5 = 2.4

The mean of the above numbers is 2.4

Here is how to do it one line:

Mean =	3 − 7 + 5 + 13 − 2	=	12	=  2.4
	5		5

Linear Inequalities (Quadratic Inequalites)

Solving Quadratic Inequalities

 

Quadratic

A Quadratic Equation (in Standard Form) looks like:

A Quadratic Equation in Standard Form
(a, b, and c can have any value, except that a can't be 0.)

That is an equation (=) but sometimes we need to solve inequalities like these:

Symbol		Words		Example
>		greater than		x2 + 3x > 2
<		less than		7x2 < 28
≥		greater than or equal to		5 ≥ x2 − x
≤		less than or equal to		2y2 + 1 ≤ 7y

Solving

Solving inequalities is just like a solving equations ... we do most of the same things.

When solving equations we need try to find the points, such as the ones marked "=0"

But when we solve inequalities we try to find interval(s), such as the one marked "<0"

So this is what we do:

• find the "=0" points
• in between the "=0" points, are intervals that are either
  • greater than zero (>0), or
  • less than zero (<0)
• then pick a test value to find out which it is (>0 or <0)

Here is an example:

Example: x² − x − 6 < 0

x² − x − 6 has these simple factors (because I wanted to make it easy!):

(x+2)(x−3) < 0

Firstly, let us find where it is equal to zero:

(x+2)(x−3) = 0

It is equal to zero when x = −2 or x = +3
because when x = −2, then (x+2) is zero
and when x = +3, then (x−3) is zero

So between −2 and +3, the function will either be

• always greater than zero, or
• always less than zero

We don't know which ... yet!

Let's pick a value in-between and test it:

At x=0:  x² − x − 6  =  0 − 0 − 6
=  −6

So between −2 and +3, the function is less than zero.
And that is the region we want, so...

x² − x − 6 < 0 in the interval (−2, 3)

Note: x² − x − 6 > 0 on the interval (−∞,−2) and (3, +∞)

And here is the plot of x2 − x − 6: The equation equals zero at −2 and 3 The inequality "<0" is true between −2 and 3.

What If It Doesn't Go Through Zero?

	Here is the plot of x2 − x + 1 There are no "=0" points! But that makes things easier!
Because the line does not cross through y=0, it must be either: always > 0, or always < 0 So all we have to do is test one value (say x=0) to see if it is above or below.

A "Real World" Example

A stuntman will jump off a 20 m building.

A high-speed camera is ready to film him between 15 m and 10 m above the ground.

When should the camera film him?
We can use this formula for distance and time:

d = 20 − 5t²

• d = distance above ground (m), and
• t = time from jump (seconds)

(Note: if you are curious about the formula, it is simplified from d = d₀ + v₀t + ½a₀t² , where d₀=20, v₀=0, and a₀=−9.81, the acceleration due to gravity.)
OK, let's go.

First, let us sketch the question:

The distance we want is from 10 m to 15 m: 10 < d < 15 And we know the formula for d: 10 < 20 − 5t2 < 15

Now let's solve it!

First, let's subtract 20 from both sides:

−10 < −5t² <−5

Now multiply both sides by −(1/5). But because we are multiplying by a negative number, the inequalities will change direction ... read Solving Inequalities to see why.

2 > t² > 1

To be neat, the smaller number should be on the left, and the larger on the right. So let's we swap them over (and make sure the inequalities still point correctly):

1 < t² < 2

Lastly, we can safely take square roots, since all values are greater then zero:

√1 < t < √2

We can tell the film crew:

"Film from 1.0 to 1.4 seconds after jumping"

Higher Than Quadratic

The same ideas can help us solve more complicated inequalities:

Example: x³ + 4 ≥ 3x² + x

First, let's put it in standard form:

x³ − 3x² − x + 4 ≥ 0

This is a cubic equation (the highest exponent is a cube, i.e. x³), and is hard to solve, so let us graph it instead:

The zero points are approximately:

• −1.1
• 1.3
• 2.9

And from the graph we can see the intervals where it is greater than (or equal to) zero:

• From −1.1 to 1.3, and
• From 2.9 on

 

 

 

In interval notation we can write:

Approximately: [−1.1, 1.3] U [2.9, +∞)

for more example I give a video

Linear Inequalities

Introduction to Inequalities

Inequality tells us about the relative size of two values.

Mathematics is not always about "equals"! Sometimes we only know that something is bigger or smaller

Example: Alex and Billy have a race, and Billy wins!

What do we know?
We don't know how fast they ran, but we do know that Billy was faster than Alex:

Billy was faster than Alex

We can write that down like this:

b > a

(Where "b" means how fast Billy was, ">" means "greater than", and "a" means how fast Alex was)

We call things like that inequalities (because they are not "equal")

Greater or Less Than

The two most common inequalities are:

Symbol	Words	Example Use
>	greater than	5 > 2
<	less than	7 < 9

They are easy to remember: the "small" end always points to the smaller number, like this:

Greater Than Symbol: BIG > small

 

Example: Alex plays in the under 15s soccer. How old is Alex?

We don't know exactly how old Alex is, because it doesn't say "equals"
But we do know "less than 15", so we can write:

Age < 15

The small end points to "Age" because the age is smaller than 15.

... Or Equal To!

We can also have inequalities that include "equals", like:

Symbol	Words	Example Use
≥	greater than or equal to	x ≥ 1
≤	less than or equal to	y ≤ 3

Example: you must be 13 or older to watch a movie.

The "inequality" is between your age and the age of 13.

Your age must be "greater than or equal to 13", which is written:

Age ≥ 13

 

*prefer use google chrome browser for watched the video*

 

 

 

Properties of Inequalities

Inequality tells us about the relative size of two values.

(You might like to read a gentle Introduction to Inequalities first)

The 4 Inequalities

Symbol	Words	Example
>	greater than	x+3 > 2
<	less than	7x < 28
≥	greater than or equal to	5 ≥ x-1
≤	less than or equal to	2y+1 ≤ 7

The symbol "points at" the smaller value

Properties

Inequalities have properties ... all with special names!
Here we list each one, with examples.
Note: the values a, b and c we use below are Real Numbers.

Transitive Property

When we link up inequalities in order, we can "jump over" the middle inequality.

If a < b and b < c, then a < c

Likewise:

If a > b and b > c, then a > c

Example:

• If Alex wong is older than Billy and
• Billy is older than Carol,

then Alex must be older than Carol also!

Reversal Property

We can swap a and b over, if we make sure the symbol still "points at" the smaller value.

• If a > b then b < a
• If a < b then b > a

Example: Alex is older than Billy, so Billy is younger than Alex

Law of Trichotomy

The "Law of Trichotomy" says that only one of the following is true:

It makes sense, right? a must be either less than b or equal to b or greater than b. It must be one of those, and only one of those.

Example: Alex wong Has More Money Than Billy

We could write it like this:

a > b

So we also know that:

• Alex wong does not have less money than Billy (not a<b)
• Alex wong does not have the same amount of money as Billy (not a=b)

(Of course!)

Addition and Subtraction

Adding c to both sides of an inequality just shifts everything along, and the inequality stays the same.

If a < b, then a + c < b + c

Example: Alex wong has less coins than Billy.

If both Alex wong and Billy get 3 more coins each, Alex wong will still have less coins than Billy.

Likewise:

• If a < b, then a − c < b − c
• If a > b, then a + c > b + c, and
• If a > b, then a − c > b − c

So adding (or subtracting) the same value to both a and b will not change the inequality

Multiplication and Division

When we multiply both a and b by a positive number, the inequality stays the same.
But when we multiply both a and b by a negative number, the inequality swaps over!

Notice that a<b becomes b<a after multiplying by (-2)
But the inequality stays the same when multiplying by +3

Here are the rules:

• If a < b, and c is positive, then ac < bc
• If a < b, and c is negative, then ac > bc (inequality swaps over!)

A "positive" example:

Example: Alex's score of 3 is lower than Billy's score of 7.

a < b

If both Alex wong and Billy manage to double their scores (×2), Alex's score will still be lower than Billy's score.

2a < 2b

But when multiplying by a negative the opposite happens:

But if the scores become minuses, then Alex wong loses 3 points and Billy loses 7 points
So Alex wong has now done better than Billy!

-a > -b

Why does multiplying by a negative reverse the sign?

Well, just look at the number line!
For example, from 3 to 7 is an increase, but from -3 to -7 is a decrease.

-7 < -3	7 > 3

See how the inequality sign reverses (from < to >) ?

Additive Inverse

As we just saw, putting minuses in front of a and b changes the direction of the inequality. This is called the "Additive Inverse":

• If a < b then -a > -b
• If a > b then -a < -b

This is really the same as multiplying by (-1), and that is why it changes direction.

Example: Alex wong  has more money than Billy, and so Alex wong is ahead.
But a new law says "all your money is now a debt you must repay with hard work"
So now Alex wong is worse off than Billy.

Multiplicative Inverse

Taking the reciprocal (1/value) of both a and b can change the direction of the inequality. When a and b are both positive or both negative: If a < b then 1/a > 1/b If a > b then 1/a < 1/b

Example: Alex wong and Billy both complete a journey of 12 kilometers.

Alex runs at 6 km/h  and Billy walks at 4 km/h.
Alex’s speed is greater than Billy’s speed

6 > 4

But Alex’s time is less than Billy’s time:

12/6 < 12/4

2 hours < 3 hours

But when either a or b is negative (not both) the direction stays the same:

• If a < b then 1/a < 1/b
• If a > b then 1/a > 1/b

Non-Negative Property of Squares

A square of a number is greater than or equal to zero:

a² ≥ 0

Example:

• (3)² = 9
• (-3)² = 9
• (0)² = 0

Always greater than (or equal to) zero

Square Root Property

Taking a square root will not change the inequality (but only when both a and b are greater than or equal to zero).

If a ≤ b then √a ≤ √b(for a,b ≥ 0)

Example: a=4, b=9

• 4 ≤ 9 so √4 ≤ √9

  

 

Probability

                                                Probability

Many events is hard to predicted with total certainty and it ide called probability..


example

Tossing a Coin  When a coin is tossed, there are two possible outcomes either head or tails. heads (H) or tails (T) We can say that the probability of the coin landing H is ½. And the probability of the coin landing T is ½. Throwing Dice  When a single die is thrown, there can be a six possible outcomes: 1, 2, 3, 4, 5, 6. The probability of any one of them is 1/6. The probability of any one of them is 1/6. Example: Deck of Cards the 5 of Clubs is a sample point the King of Hearts is a sample point "King" is not a sample point. As there are 4 Kings that is 4 different sample points.   Probability   Probability of an event happening = Number of ways it can happen Total number of outcomes Example: the chances of rolling a "4" with a die Number of ways it can happen: 1 (there is only 1 face with a "4" on it) Total number of outcomes: 6 (there are 6 faces altogether) So the probability = 1 6 Example: there are 5 marbles in a bag: 4 are blue, and 1 is red. What is the probability that a blue marble gets picked? Number of ways it can happen: 4 (there are 4 blues) Total number of outcomes: 5 (there are 5 marbles in total) So the probability = 4 5 = 0.8   There is several type of event for probability Independent Events Dependent Events Tree Diagrams Example Events: Getting a Tail when tossing a coin is an event Rolling a "5" is an event. An event can include several outcomes: Choosing a "King" from a deck of cards (any of the 4 Kings) is also an event Rolling an "even number" (2, 4 or 6) is an event. Events can be: Independent (each event is not affected by other events), Dependent (also called "Conditional", where an event is affected by other events) Mutually Exclusive (events can't happen at the same time) Independent Events Events can be "Independent", which mean   each of the event is not affected by any other events. This is an important idea! A coin did not "know" that it came up heads before ... each toss of a coin is a perfect isolated thing Example: You toss a coin three times and it comes up "Heads" each time ... what is the chance that the next toss will also be a "Head"? The chance is simply 1/2, or 50%, just like ANY OTHER toss of the coin. What it did in the past will not affect the current toss! Dependent Events But some events can be "dependent" ... which means they can be affected by previous events. Example: Drawing 2 Cards from a Deck After taking one card from the deck there are less cards available, so the probabilities change! Let's look at the chances of getting a King. For the 1st card the chance of drawing a King is 4 out of 52 But for the 2nd card: If the 1st card was a King, then the 2nd card is less likely to be a King, as only 3 of the 51 cards left are Kings. If the 1st card was not a King, then the 2nd card is slightly more likely to be a King, as 4 of the 51 cards left are King. Tree Diagrams  When we have Dependent Events it helps to make a "Tree Diagram" Example: Soccer Game You are off to soccer, and love being the Goalkeeper, but that depends who is the Coach today: with Coach Sam your probability of being Goalkeeper is 0.5 with Coach Alex your probability of being Goalkeeper is 0.3 Sam is Coach more often ... about 6 of every 10 games (a probability of 0.6). Start with the Coaches. We know 0.6 for Sam, so it must be 0.4 for Alex (the probabilities must add to 1): Then fill out the branches for Sam (0.5 Yes and 0.5 No), and then for Alex (0.3 Yes and 0.7 No): Now it is neatly laid out we can calculate probabilities (read more at "Tree Diagrams"). This is video of probability