Combinations and Permutations
What's the Difference?
we use the word "combination" loosely, without thinking if the order of things is important. In other words:| "My fruit salad is a combination of apples, grapes and bananas" We don't care what order the fruits are in, they could also be "bananas, grapes and apples" or "grapes, apples and bananas", its the same fruit salad. | |
| "The combination to the safe is 472". Now we do care about the order. "724" won't work, nor will "247". It has to be exactly 4-7-2. |
| If the order doesn't matter, it is a Combination. | |
| If the order does matter it is a Permutation. |
| So, we should really call this a "Permutation Lock"! |
A Permutation is an ordered Combination.
| To help you to remember, think "Permutation ... Position" this is the video |
Permutations
There are basically two types of permutation:- Repetition is Allowed: such as the lock above. It could be "333".
- No Repetition: for example the first three people in a running race. You can't be first and second.
1. Permutations with Repetition
it easiest to calculate.When we have n things to choose from ... we have n choices each time!
When choosing r of them, the permutations are:
n × n × ... (r times)
(In other words, there are n possibilities for the first choice, THEN there are n possibilites for the second choice, and so on, multplying each time.)Which is easier to write down using an exponent of r:
n × n × ... (r times) = nr
Example: in the lock above, there are 10 numbers to choose from (0,1,...9) and we choose 3 of them:
So, the formula is simply:
10 × 10 × ... (3 times) = 103 = 1,000 permutations
| nr |
| where n is the number of things to choose from, and we choose r of them (Repetition allowed, order matters) |
2. Permutations without Repetition
In this case, we have to reduce the number of available choices each time.After choosing, say, number "14" we can't choose it again.
So, our first choice has 16 possibilites, and our next choice has 15 possibilities, then 14, 13, etc. And the total permutations are:
16 × 15 × 14 × 13 × ... = 20,922,789,888,000
But maybe we don't want to choose them all, just 3 of them, so that is only:
16 × 15 × 14 = 3,360
In other words, there are 3,360 different ways that 3 pool balls could be arranged out of 16 balls.
Without repetition our choices get reduced each time.
But how do we write that mathematically? Answer: we use the "factorial function"The factorial function (symbol: !) just means to multiply a series of descending natural numbers. Examples:
| |
| Note: it is generally agreed that 0! = 1. It may seem funny that multiplying no numbers together gets us 1, but it helps simplify a lot of equations. | |
16! = 20,922,789,888,000
But when we want to select just 3 we don't want to multiply after 14. How do we do that? There is a neat trick ... we divide by 13! ...
16 × 15 × 14 × 13 × 12 ...
| = 16 × 15 × 14 = 3,360 | |
13 × 12 ...
|
The formula is written:
| where n is the number of things to choose from, and we choose r of them (No repetition, order matters) |
Examples:
Our "order of 3 out of 16 pool balls example" is:| 16! | = | 16! | = | 20,922,789,888,000 | = 3,360 |
| (16-3)! | 13! | 6,227,020,800 |
(which is just the same as: 16 × 15 × 14 = 3,360)
How many ways can first and second place be awarded to 10 people?| 10! | = | 10! | = | 3,628,800 | = 90 |
| (10-2)! | 8! | 40,320 |
(which is just the same as: 10 × 9 = 90)
Notation
Instead of writing the whole formula, people use different notations such as these:
Example: P(10,2) = 90
Combinations
There are also two types of combinations (remember the order is not important now): 1.Repetition Allowed: such as coins in your pocket (5,5,5,10,10) 2.No Birthday: such as lottery numbers (2,14,15,27,30,33) 1. Combination with repetition In fact, this is the most difficult to explain, so they will come back to this later. 2. Combination without repetition This is how the lottery works. The numbers are drawn one by one, and if we are lucky numbers (no matter what order) to win! The easiest way to explain it is: • it assumes that the order does not matter (ie permutations) • then modify it so that the order is not important. Returning to the example of a ball, let's say you just want to know that three billiard balls, is not selected. We already know that 3 out of 16 gives us 3360 permutations. But many people are just like now, because no matter the order! For example, they say balls 1, 2 and 3 are selected. This is possible: Order does not matter the order is not important 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 1 2 3 Therefore, the permutations will have 6 times more likely. In fact, there is no easy way to figure out how many ways "1 2 3" can be put in order, and we were talking about. The answer is: 3! = 3 × 2 × 1 = 6 (Another example: 4 things that can be placed in 4 = 4 × 3 × 2 × 1 = 24 different ways, try it for yourself!) Therefore, we adjust our permutations formula to reduce it by the number of ways in which objects can be in order (because we are not interested in your message more):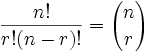 |
| where n is the number of things to choose from, and we choose r of them (No repetition, order doesn't matter) |
It is often called "n choose r" (such as "16 choose 3")
And is also known as the Binomial Coefficient.
And is also known as the Binomial Coefficient.
Notation
As well as the "big parentheses", people also use these notations: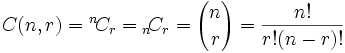
Just remember the formula:
| n! |
| r!(n−r)! |
Example
So, our pool ball example (now without order) is:| 16! | = | 16! | = | 20,922,789,888,000 | = 560 |
| 3!(16-3)! | 3!×13! | 6×6,227,020,800 |
| 16×15×14 | = | 3360 | = 560 |
| 3×2×1 | 6 |
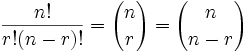
| 16! | = | 16! | = | 16! | = 560 |
| 3!(16-3)! | 13!(16-13)! | 3!×13! |
Pascal's Triangle
We can also use Pascal's Triangle to find the values. Go down to row "n" (the top row is 0), and then along "r" places and the value there is our answer. Here is an extract showing row 16:1 14 91 364 ... 1 15 105 455 1365 ... 1 16 120 560 1820 4368 ...
1. Combinations with Repetition
Well, now we can deal with this ... Say there are five ice cream flavors: banana, chocolate, lemon, strawberry and vanilla. We can have three balls. How much variation is there? We will use the letters to guess: {b, c, l, s, v}. Examples include choice • {c, c, c} (3 tablespoons brown) • {b, l, v} (each a banana, lemon and vanilla) • {b, v, v} (one banana, two vanilla) (And let's be clear: there are n = 5 things to choose from, and we chose r = 3 of them. the order is not important, and we can repeat!) Now, I can not describe to you how to calculate this, but I can show special technique that allows you to exercise. Think of ice cream in a box, we can say "leave the first frame, then take 3 tablespoons, then pass along 3 more boxes until the end" and we will have 3 tablespoons chocolate! This is how we ask the robot to get ice cream, but nothing changes, we still get what we want. We can write this as (arrow means movement, circle means scoop). In fact, all three of the above examples can be written as: {C, c, c} (3 tablespoons brown): {B, l, v} (each a banana, lemon and vanilla): {B, v, v} (one banana, two vanilla): OK, so instead of worrying about different flavors, we have a simple question: "How many different ways can arrange arrows and circles" Note that there are always 3 network (3 scoops of ice cream) and 4 arrow keys (we need to go 4 times to go 1-5 containers). So (ie generally here) there are r + (n-1) positions, and we choose r of them for a loop. This is like saying "we had a ball r + (n-1) of the pool and we choose r of them." In other words, the question is now like a billiard ball, but with the slightly modified. And we can write like this
note: r+(n−1) is the same as n+r−1):
Interestingly, we can look at the arrows instead of the circles, and say "we have r + (n−1) positions and want to choose (n−1) of them to have arrows", and the answer is the same:
where n is the number of things to choose from, and we choose r of them (Repetition allowed, order doesn't matter)
So, what about our example, what is the answer?
(5+3−1)! = 7! = 5040 = 35 3!(5−1)! 3!×4! 6×24 In Conclusion
that was a lot to absorb, so maybe you could read it again to be sure!
But knowing how these formulas work is only half the battle. Figuring out how to interpret a real world situation can be quite hard.
But at least now you know how to calculate all 4 variations of "Order does/does not matter" and "Repeats are/are not allowed".
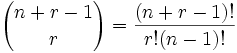
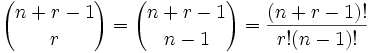
No comments:
Post a Comment