Combinations
There are also two types of combinations (remember the order does not matter now):- Repetition is Allowed: such as coins in your pocket (5,5,5,10,10)
- No Repetition: such as lottery numbers (2,14,15,27,30,33)
1. Combinations with Repetition
There are also two types of combinations (remember the order is not important now): 1.Repetition animals like coins in your pocket (5,5,5,10,10) 2.No birthday: for example, lottery numbers (2,14,15,27,30,33) 1. Combined with repetition In fact, this is the most difficult to explain, so they will come back to this later. 2. Combination without repetition Here's how it works lottery. The numbers are drawn one by one, and if we are lucky numbers (no matter what order) to win! The easiest way to explain it is: • assumed that the order is not important (ie, permutations) • then modify it so that the order is not important. Returning to the example of the ball, say what you want is to know that three billiard balls, is not selected. We already know that 3 out of 16 gives us 3360 permutations. However, many people like now, because no matter the order! For example, let's say the ball 1, 2 and 3 are selected. This may be: Order does not matter the order is not important 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 1 2 3 Therefore, the permutations will have 6 times more likely. In fact, there is no easy way to figure out how many ways "1 2 3" can be put in order, and we talk. The answer is: 3! = 3 × 2 × 1 = 6 (Another example: 4 things that can be placed in 4 = 4 × 3 × 2 × 1 = 24 different ways, try it for yourself!) Therefore, we adjust our permutations formula to reduce it by the number of ways in which objects can be in order (because we are not interested in their message more):Actually, these are the hardest to explain, so we will come back to this later.
2. Combinations without Repetition
This is how lotteries work. The numbers are drawn one at a time, and if we have the lucky numbers (no matter what order) we win!The easiest way to explain it is to:
- assume that the order does matter (ie permutations),
- then alter it so the order does not matter.
We already know that 3 out of 16 gave us 3,360 permutations.
But many of those are the same to us now, because we don't care what order!
For example, let us say balls 1, 2 and 3 are chosen. These are the possibilites:
| Order does matter | Order doesn't matter |
| 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 | 1 2 3 |
In fact there is an easy way to work out how many ways "1 2 3" could be placed in order, and we have already talked about it. The answer is:
3! = 3 × 2 × 1 = 6
(Another example: 4 things can be placed in 4! = 4 × 3 × 2 × 1 = 24 different ways, try it for yourself!)So we adjust our permutations formula to reduce it by how many ways the objects could be in order (because we aren't interested in their order any more):
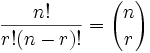 |
| where n is the number of things to choose from, and we choose r of them (No repetition, order doesn't matter) |
It is often called "n choose r" (such as "16 choose 3")
And is also known as the Binomial Coefficient.
And is also known as the Binomial Coefficient.
Notation
As well as the "big parentheses", people also use these notations: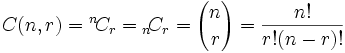
Just remember the formula:
| n! |
| r!(n−r)! |
Example
So, our pool ball example (now without order) is:| 16! | = | 16! | = | 20,922,789,888,000 | = 560 |
| 3!(16-3)! | 3!×13! | 6×6,227,020,800 |
| 16×15×14 | = | 3360 | = 560 |
| 3×2×1 | 6 |
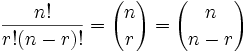
| 16! | = | 16! | = | 16! | = 560 |
| 3!(16-3)! | 13!(16-13)! | 3!×13! |
Pascal's Triangle
We can also use Pascal's Triangle to find the values. Go down to row "n" (the top row is 0), and then along "r" places and the value there is our answer. Here is an extract showing row 16:1 14 91 364 ... 1 15 105 455 1365 ... 1 16 120 560 1820 4368 ...
1. Combinations with Repetition
OK, now we can tackle this one ...
We can have three scoops. How many variations will there be?
Let's use letters for the flavors: {b, c, l, s, v}. Example selections include
- {c, c, c} (3 scoops of chocolate)
- {b, l, v} (one each of banana, lemon and vanilla)
- {b, v, v} (one of banana, two of vanilla)
(And just to be clear: There are n=5 things to choose from, and we choose r=3 of them.
Order does not matter, and we can repeat!)
Now, I can't describe directly to you how to calculate this, but I can show you a special technique that lets you work it out.Order does not matter, and we can repeat!)
Think about the ice cream being in boxes, we could say "move past the first box, then take 3 scoops, then move along 3 more boxes to the end" and we will have 3 scoops of chocolate!
So it is like we are ordering a robot to get our ice cream, but it doesn't change anything, we still get what we want.We can write this down as
In fact the three examples above can be written like this:
| {c, c, c} (3 scoops of chocolate): | |
| {b, l, v} (one each of banana, lemon and vanilla): | |
| {b, v, v} (one of banana, two of vanilla): |
Notice that there are always 3 circles (3 scoops of ice cream) and 4 arrows (we need to move 4 times to go from the 1st to 5th container).
So (being general here) there are r + (n−1) positions, and we want to choose r of them to have circles.
This is like saying "we have r + (n−1) pool balls and want to choose r of them". In other words it is now like the pool balls question, but with slightly changed numbers. And we can write it like this (note: r+(n−1) is the same as n+r−1):
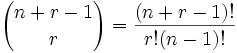 |
| where n is the number of things to choose from, and we choose r of them (Repetition allowed, order doesn't matter) |
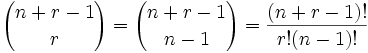
| (5+3−1)! | = | 7! | = | 5040 | = 35 |
| 3!(5−1)! | 3!×4! | 6×24 |
In Conclusion
Phew, that was a lot to absorb, so maybe you could read it again to be sure!But knowing how these formulas work is only half the battle. Figuring out how to interpret a real world situation can be quite hard.
But at least now you know how to calculate all 4 variations of "Order does/does not matter" and "Repeats are/are not allowed".